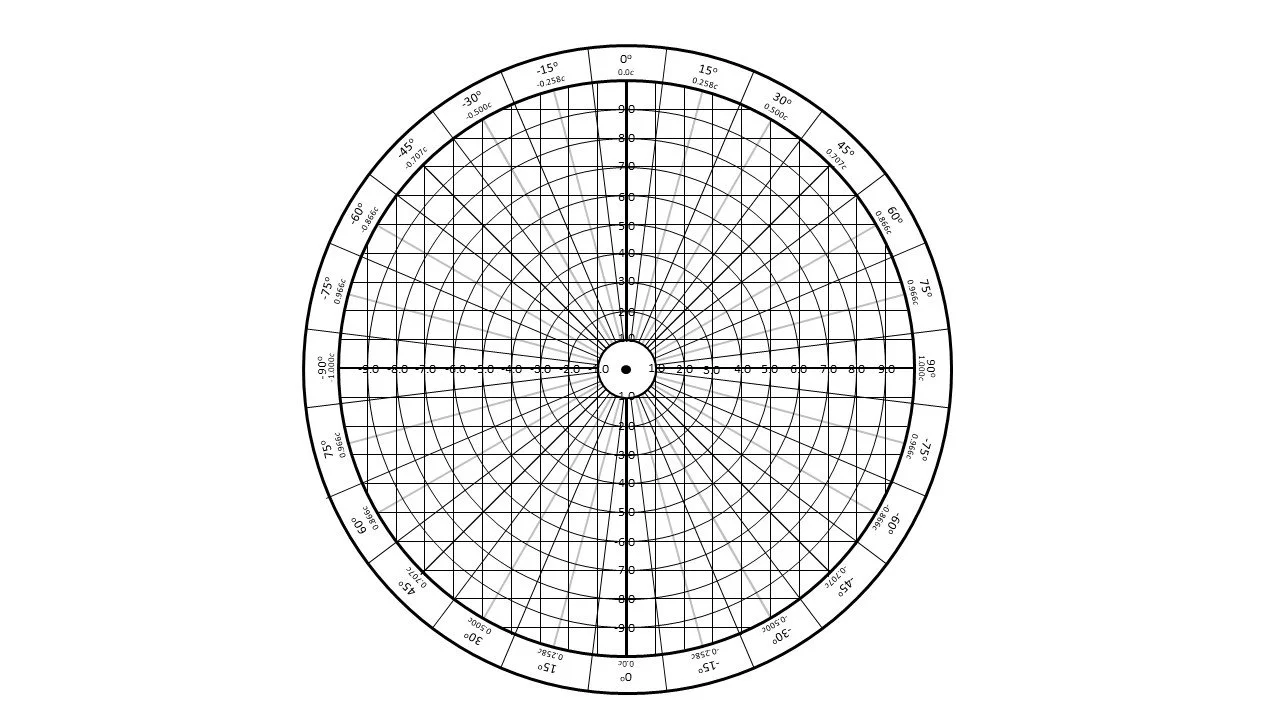
The Relativity Polar Plot consists of ten concentric circles with the radial distance representing units of distance for time ct or spatial x, overlaying a rectangular grid of the same measure. The radial lines correspond to the angle from zero, the sine of which equals v/c, so marked every 15 degrees. The upper hemisphere represents positive time from 0 at the center, for opening velocities, while the bottom hemisphere represents negative time before zero, for closing velocities. Bodies are collocated the origin. The direction of time for each body corresponds to its radial line, with its x-axis perpendicular to it. Let us take as an example two bodies separating at half the speed of light. We may assign, for convenience, one body’s time axis to the zero degree radial with the x-axis at 90 degrees. The other body’s time axis will then lie on the +30 (opening to the right) or -30 degree radial (opening to the left), with its x-axis at 120 or 60 degrees. Closing velocity scenarios are obtained by extending the time axis through the origin into the bottom half. A body opening to the right aft collocation at the center will be approaching from the left prior to collocation.

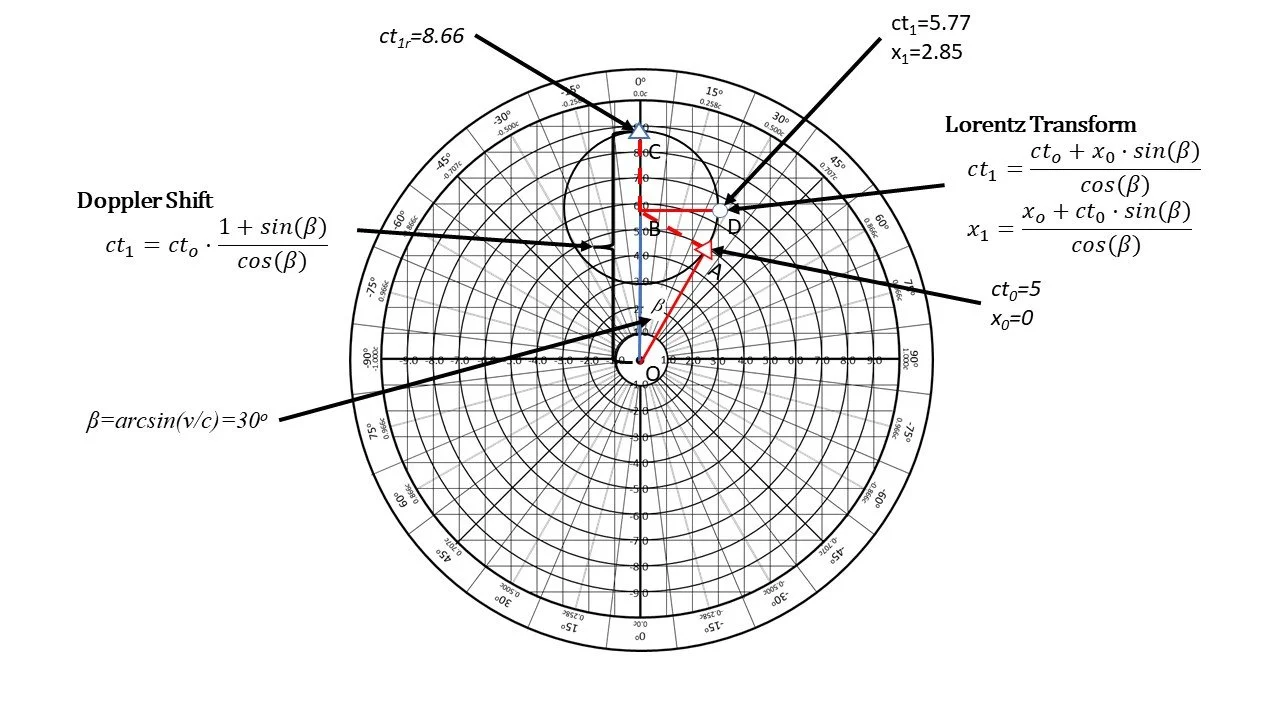
Let’s do a quick sample problem. Let’s examine two bodies. S0 and S1, at a relative velocity of half the speed of light, a velocity angle beta of 30 degrees. We erect S1’s time axis on the zero degree radial in blue, and S0 on the 30 degree radial in red. We locate an event in S0 at ct=5 and x=0, marked as a red triangle at A. When will S1 see this event, and where will it locate it?

We draw a dashed red line from A perpendicular to the S0 time axis, to intercept the time axis of S1 at B, then an equal distance along the S1 time axis, to locate the time of receipt at C. The time interval OC is the relativistic Doppler shift , shown trigonometrically in terms of beta, of the time of transmission of the event OA along path ABC, with a value of 8.66. S1 will locate the event at D, with time equal to OB, 5.77, and x=BD=2.85, thus ensuring that S1 measures the speed of light based on its measurement along path DBC, regardless of the velocity of S0. D is the Lorentz Transform of A, shown trigonometrically. S1 can determine the proper time of the event by solving the velocity triangle OAB, subtracting the square of its measured distance BD equal to BA, from the square of its measured time OB, and taking the square root to determine OA.

Note that both S0 and S1 have equal units of measure, and their x-axes are normal to their time axes. Additional reference frame can easily be added to this plot to see their observations and measurements of events and measurements in S0 and S1.